8 Algorithms

8.1 Maximum likelihood estimation

8.1.1 Likelihood estimation

(without random effects)

With the normal distribution of errors, likelihood can be expressed explicitly as the product of the densities of each of the $n$ independent normal observations.
$$\ell =-\log L$$

• the negative log-likelihood $$\begin{array}{cc}\ell ((y_1,\dots ,y_n),\mu ,{\sigma }^2)& =-\log \left[\prod _{i=1}^n\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{{(y_i-\mu )}^2}{2{\sigma }^2})\right]\\ & =-\sum _{i=1}^n[\log \left(\frac{1}{\sqrt{2\pi {\sigma }^2}}\right)+(-\frac{{(y_i-\mu )}^2}{2{\sigma }^2})]\end{array}$$ then,

• for matrix format

$$\begin{array}{cc}\ell (y,\beta ,\gamma )& =\frac{1}{2}\left\{n\log \right(2\pi )+\log \left|{\sigma }^{2}I\right|+(y-X\beta {)}^{\prime }{\left({\sigma }^{2}I\right)}^{-1}(y-X\beta )\}\\ & =\frac{1}{2}\left\{n\log \right(2\pi )+\log \left(\prod _{i=1}^n{\sigma }^2\right)+(y-X\beta {)}^{\prime }(y-X\beta )/{\sigma }^2\}\\ & =\frac{1}{2}\left\{n\log \right(2\pi )+n\log \left({\sigma }^2\right)+(y-\mu {)}^{\prime }(y-\mu )/{\sigma }^2\}\\ & =\frac{1}{2}\left\{n\log \right(2\pi )+n\log \left({\sigma }^2\right)+\sum _{i=1}^n{(y_i-\mu )}^2/{\sigma }^2\}\end{array}$$ where $\gamma$ derived from ${\sigma }^{2}I$.

• minimize $\ell$ by taking the derivative $$argmin\left(\ell \right(y,\beta ,\gamma \left)\right)$$

taking the derivatives of the negative log-likelihood function.

$$\begin{array}{cc}\frac{\partial \ell (\mu ,{\sigma }^2)}{\partial \mu }& =\frac{1}{2}\left[\sum _{i=1}^n\right(-2\left)(y_i-\mu )/{\sigma }^2\right]\\ & =(n\mu -\sum _{i=1}^n{y}_i)/{\sigma }^2=0\end{array}$$

$$\frac{\partial \ell (\mu ,{\sigma }^2)}{\partial {\sigma }^2}=\frac{1}{2}[\frac{n}{{\sigma }^2}-\frac{{\sum }_{i=1}^n{(y_i-\mu )}^2}{{\left({\sigma }^2\right)}^2}]=0$$

setting the derivatives equal to zero and solving for the parameters

$$\begin{array}{cc}\hat{\mu }& =\overline{y}\\ {\hat{\sigma }}^2& =\frac{1}{n}\sum _{i=1}^n{(y_i-\mu )}^2\\ & =\frac{1}{n}\sum _{i=1}^n{(y_i-\overline{y})}^2\end{array}$$

but for REML $$\begin{array}{cc}{\hat{\sigma }}^2& =\frac{1}{n-1}\sum _{i=1}^n{(y_i-\mu )}^2\\ & =\frac{1}{n-1}\sum _{i=1}^n{(y_i-\overline{y})}^2\end{array}$$

8.1.2 R demonstration

• toy data

set.seed(123)
n <- 20000
x <- rnorm(n, 2, sqrt(2))
s <- rnorm(n, 0, 0.8)
y <- 1.5+x*3+s
mydata <- data.frame(y,x)

• using linear regression

lmfit <- lm(y~., data=mydata)
# logLik(lmfit)
coefficients(lmfit)

## (Intercept)           x 
##    1.487701    3.003695

(summary(lmfit)$sigma**2)

## [1] 0.6397411

• using -log max likelihood estimate formula

notice, using vector and matrix notation

 ## Using the mathematical expression:
 minusloglik <- function(param){
   beta <- param[-1] #Regression Coefficients
   sigma <- param[1] #Variance
   y <- as.vector(mydata$y) #DV
   x <- cbind(1, mydata$x) #IV
   mu <- x%*%beta #multiply matrices
   0.5*(n*log(2*pi) + n*log(sigma) + sum((y-mu)^2)/sigma)
 }

MLoptimize <- optim(  c (1,  1, 1 ), minusloglik)
## The results:
MLoptimize$par

## [1] 0.6397201 1.4876186 3.0038675

• using max likelihood estimate directly (normal distribution)

# max 
library(maxLik)
ols.lf <- function(param) {
  beta <- param[-1] #Regression Coefficients
  sigma <- param[1] #Variance
  y <- as.vector(mydata$y) #DV
  x <- cbind(1, mydata$x) #IV
  mu <- x%*%beta #multiply matrices
  sum(dnorm(y, mu, sqrt(sigma), log = TRUE)) #normal distribution(vector of observations, mean, sd)
}  

mle_ols <- maxLik(logLik = ols.lf, start = c(sigma = 1, beta1 = 1, beta2 = 1 ))
summary(mle_ols)

## --------------------------------------------
## Maximum Likelihood estimation
## Newton-Raphson maximisation, 11 iterations
## Return code 8: successive function values within relative tolerance limit (reltol)
## Log-Likelihood: -23910.85 
## 3  free parameters
## Estimates:
##       Estimate Std. error t value Pr(> t)    
## sigma 0.639677   0.006396   100.0  <2e-16 ***
## beta1 1.487701   0.009768   152.3  <2e-16 ***
## beta2 3.003695   0.003999   751.2  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## --------------------------------------------

• another example

ols.lf <- function(param) {
  beta <- param[-1] #Regression Coefficients
  sigma <- param[1] #Variance
  y <- as.vector(mtcars$mpg) #DV
  x <- cbind(1, mtcars$cyl, mtcars$disp) #IV
  mu <- x%*%beta #multiply matrices
  sum(dnorm(y, mu, sqrt(sigma), log = TRUE)) #normal distribution(vector of observations, mean, sd)
}  

mle_ols <- maxLik(logLik = ols.lf, start = c(sigma = 1, beta1 = 1, beta2 = 1, beta3=1))
summary(mle_ols)

## --------------------------------------------
## Maximum Likelihood estimation
## Newton-Raphson maximisation, 28 iterations
## Return code 2: successive function values within tolerance limit (tol)
## Log-Likelihood: -79.57282 
## 4  free parameters
## Estimates:
##        Estimate Std. error t value   Pr(> t)    
## sigma  8.460632   2.037359   4.153 0.0000329 ***
## beta1 34.661013   2.395871  14.467   < 2e-16 ***
## beta2 -1.587281   0.673675  -2.356    0.0185 *  
## beta3 -0.020584   0.009757  -2.110    0.0349 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## --------------------------------------------

#Checking against linear regression
lmfit2 <- (lm(mpg~cyl+disp, data=mtcars))
lmfit2

## 
## Call:
## lm(formula = mpg ~ cyl + disp, data = mtcars)
## 
## Coefficients:
## (Intercept)          cyl         disp  
##    34.66099     -1.58728     -0.02058

(summary(lmfit2)$sigma**2)

## [1] 9.335872

8.1.3 Estimate confidence intervals using the likelihood

Most classical confidence intervals for parameters are estimated using the likelihood approach, the Wald interval (or the asymptotic normality property).

$${\hat{\theta }}_i\pm z_{1-\alpha /2}S{E}_{{\hat{\theta }}_i}$$

where the standard error is from the second derivative of the log-likelihood function. This is the Hessian matrix/(observed) Information matrix if there is more than one single model parameter.

• take second derivative of the log-likelihood function

$$I\left(\theta \right)={\ell }^{\prime \prime }\left(\theta \right)$$

e.g. for one independent variable (with parameters: $\beta$ and ${\sigma }^2$ in the model).

Here, giving the four entries of the $2\times 2$ Hessian matrix $$\frac{{\partial }^2\ell (\mu ,{\sigma }^2)}{\partial {\mu }^2}=\frac{n}{{\sigma }^2}$$ $$\frac{{\partial }^2\ell (\mu ,{\sigma }^2)}{\partial \left({\sigma }^2\right)}=\sqrt{\frac{2{\left({\hat{\sigma }}^2\right)}^2}{n}}$$

$$\frac{{\partial }^2\ell (\mu ,{\sigma }^2)}{\partial \mu \partial \left({\sigma }^2\right)}=0\frac{{\partial }^2\ell (\mu ,{\sigma }^2)}{\partial \left({\sigma }^2\right)\partial \mu }=0$$

therefore $$S{E}_{{\hat{\theta }}_i}=\sqrt{{\left(I\right(\hat{\theta }{)}^{-1})}_i}$$

the inverse of the Fisher information is just each diagonal element, so

• For $\beta$ $$S{E}_{\hat{\mu }}=\sqrt{{\left(I{(\hat{\mu },{\hat{\sigma }}^2)}^{-1}\right)}_{11}}=\sqrt{\frac{{\hat{\sigma }}^2}{n}}$$ Thus, the Wald confidence interval for the mean would be $${\hat{u}}^2\pm z_{1-\alpha /2}\sqrt{\frac{{\hat{\sigma }}^2}{n}}$$

• For variance $$S{E}_{{\hat{\sigma }}^2}=\sqrt{{\left(I{(\hat{\mu },{\hat{\sigma }}^2)}^{-1}\right)}_{22}}=\sqrt{\frac{2{\left({\hat{\sigma }}^2\right)}^2}{n}}$$

Thus, the Wald confidence interval for the variance would be $${\hat{\sigma }}^2\pm z_{1-\alpha /2}{\hat{\sigma }}^2\sqrt{\frac{2}{n}}$$

However, the following approach confidence interval will generally have much better small sample properties than the Wald interval.

$$\{\theta \mid \frac{L\left(\theta \right)}{L\left(\hat{\theta }\right)}>\exp (-3.84/2\left)\right\}$$

8.1.4 The profile likelihood

It can be profiled by maximizing the likelihood function with respect to all the other parameters.

In the following equation, ${\sigma }^2$ expressed by $\mu$

$$\begin{array}{cc}{L}_p\left(\mu \right)& =L(\mu ,\frac{1}{n}\sum _{i=1}^n{(y_i-\mu )}^2)\\ & =\prod _{i=1}^n\frac{1}{\sqrt{2\pi \frac{1}{n}{\sum }_{i=1}^n{(y_i-\mu )}^2}}\exp (-\frac{{(y_i-\mu )}^2}{2\frac{1}{n}{\sum }_{i=1}^n{(y_i-\mu )}^2})\end{array}$$

Similarly, the profile likelihood for the variance ${\sigma }^2$ can be expressed $$\begin{array}{cc}{L}_p\left({\sigma }^2\right)& =L(\hat{\mu }\left({\sigma }^2\right),{\sigma }^2)\\ & =L(\overline{y},{\sigma }^2)\end{array}$$

This becomes particularly simple, as the $u$-estimate does not depend on the $\sigma$.

8.1.5 Maximum likelihood estimate practice

question: eatimate mean and variance

sample<-c(1.38, 3.96, -0.16, 8.12, 6.30, 2.61, -1.35, 0.03, 3.94, 1.11)
n<-length(sample)
muhat<-mean(sample)
sigsqhat<-sum((sample-muhat)^2)/n
muhat

## [1] 2.594

sigsqhat

## [1] 8.133884

loglike<-function(theta){
a<--n/2*log(2*pi)-n/2*log(theta[2])-sum((sample-theta[1])^2)/(2*theta[2])
return(-a)
}
optim(c(2,2),loglike,method="BFGS")$par

## [1] 2.593942 8.130340

8.2 Gradient descent

• linear regression

library("ggplot2")
# fit a linear model
res <- lm( hwy ~ cty ,data=mpg)
summary(res)

## 
## Call:
## lm(formula = hwy ~ cty, data = mpg)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -5.3408 -1.2790  0.0214  1.0338  4.0461 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.89204    0.46895   1.902   0.0584 .  
## cty          1.33746    0.02697  49.585   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.752 on 232 degrees of freedom
## Multiple R-squared:  0.9138, Adjusted R-squared:  0.9134 
## F-statistic:  2459 on 1 and 232 DF,  p-value: < 2.2e-16

• compute regression coefficients

# squared error cost function
cost <- function(X, y, theta) {
  sum( (X %*% theta - y)^2 ) / (2*length(y))
}

# learning rate and iteration limit
alpha <- 0.005
num_iters <- 20000

# keep history
cost_history <- double(num_iters)
theta_history <- list(num_iters)

# initialize coefficients
theta <- matrix(c(0,0), nrow=2)

x=mpg$cty
y=mpg$hwy

# add a column of 1's for the intercept coefficient
X <- cbind(1, matrix(x))

# gradient descent
for (i in 1:num_iters) {
  error <- (X %*% theta - y)
  delta <- t(X) %*% error / length(y)   #derivation
  
  theta <- theta - alpha * delta
  
  cost_history[i] <- cost(X, y, theta)
  theta_history[[i]] <- theta
}

print(theta)

##           [,1]
## [1,] 0.8899161
## [2,] 1.3375742

tail(cost_history)

## [1] 1.522137 1.522137 1.522137 1.522137 1.522137 1.522137

• plot the cost function

plot(cost_history, type='line', col='red', lwd=2, main='Cost function', ylab='cost', xlab='Iterations')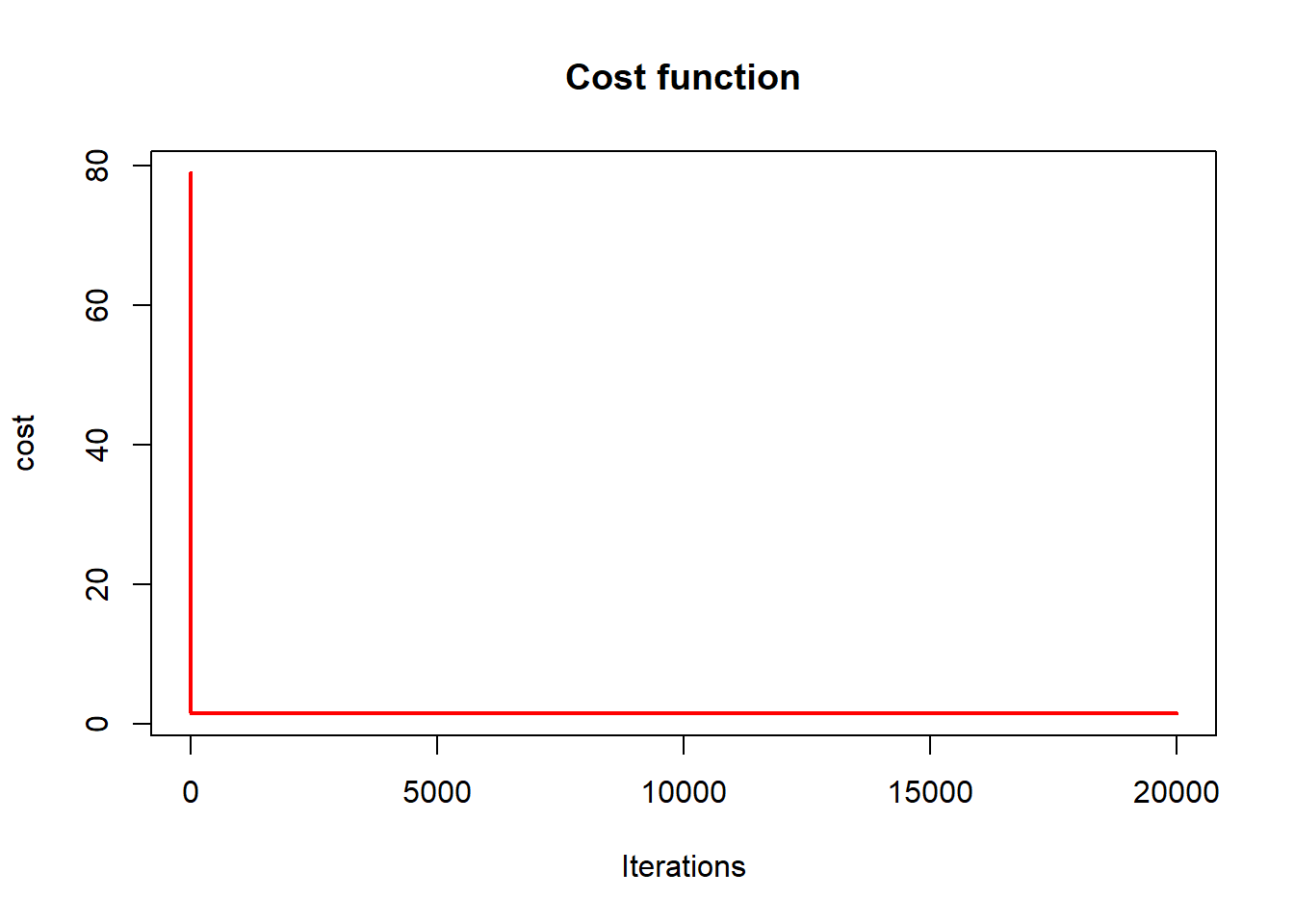

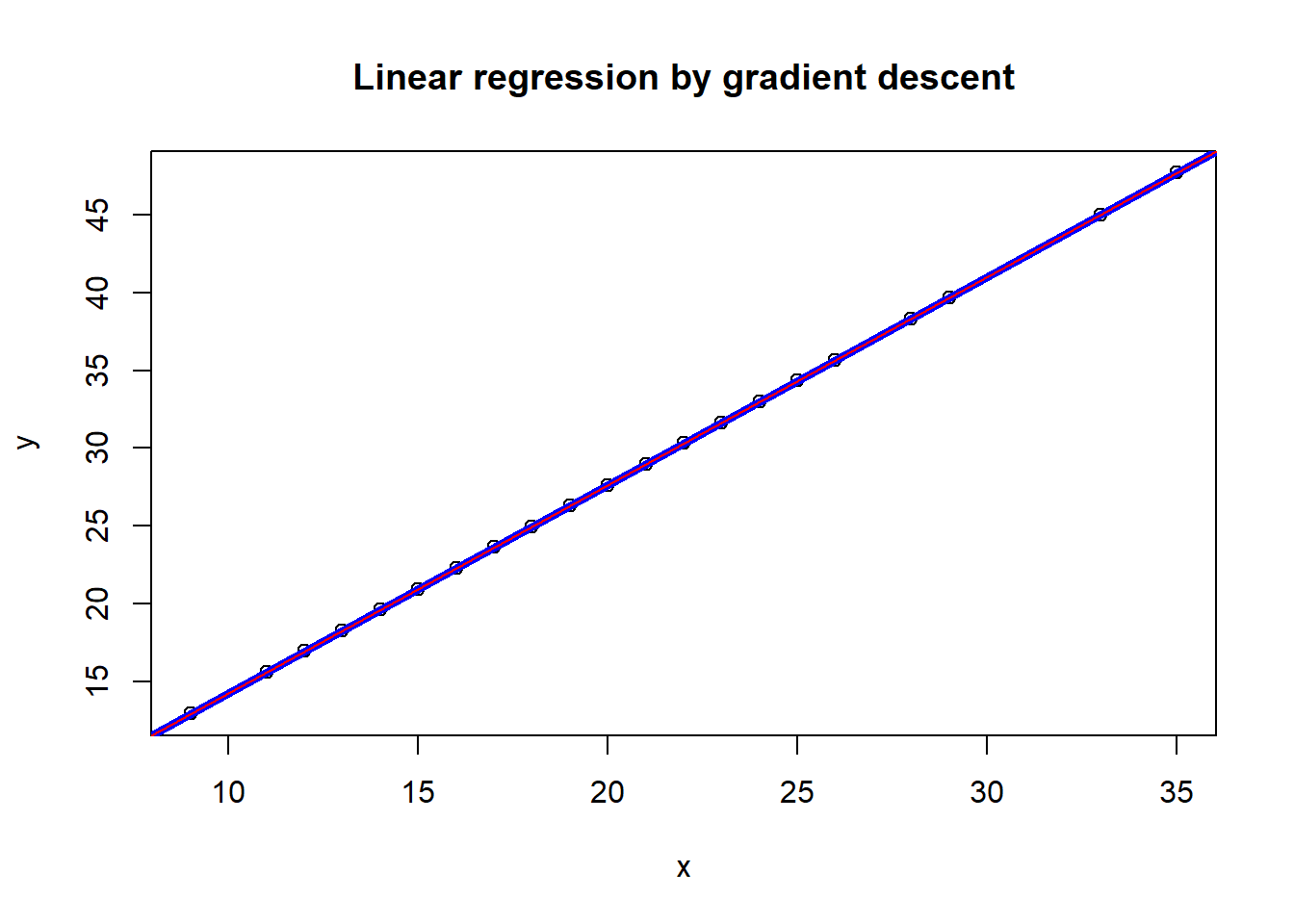
- compare two ways (linear regresion vs. gradient descent)

x=mpg$cty
y=mpg$cty*theta[2]  +  theta[1]
plot(x,y, main='Linear regression by gradient descent')
# line(x,y ,col=3)
abline(lm(mpg$hwy ~ mpg$cty),col="blue",lwd = 4)
abline(res, col='red')

8.3 Markov chain Monte Carlo

see here

8.4 Expectation maximum

see here

8.5 Combine estimates by pooling rules

see here

8.6 Simulations and Bootstrapping

see here