7 Probability

7.1 Probability basics

7.1.1 Events

Probability is the likelihood of an outcome. e.g. {any combination of two dice}
Event is a collection of outcomes. e.g. {both dice show the same face}
The outcome space is all the possible outcomes. e.g. {all the possible outcomes die show}

7.1.2 Probability formulas

discrete variable

$P (E) = \frac{n u m b e r o f o u t c o m e s i n E}{n u m b e r o f p o s s i b l e o u t c o m e s}$

continuous varable

$P (\begin{matrix} a \leq X \leq b \end{matrix}) = \int_{a}^{b} f (x) d x$ Probabilities of continuous random variables (X) are the area under the curve. The probability of any value is always zero. when X = k,

$P (\begin{matrix} X = k \end{matrix}) = 0$

7.1.3 Calculation of probability (operations)

union probability, addition rule + $\begin{aligned} P (A \cup B) = P (A) + P (B) - P (A \cap B) \\ P (A \cup B) = P (A) + P (B) if A and B are mutually exclusive \end{aligned}$ joint probability, multiple rule x $\begin{aligned} P (A \cap B) = P (A ∣ B) P (B) = P (B ∣ A) P (A) \\ P (A \cap B) = P (A) P (B) if A and B are independent \end{aligned}$ Marginal Probability is without reference to any other event or events $P (A) o r P (B)$

conditional Probability $P (A ∣ B) = \frac{P (A \cap B)}{P (B)}$ p-values are conditional probabilities.

7.1.4 Bayes’s theorem

multiple law $P (A \cap B) = P (A | B) P (B) = P (B | A) P (A)$
bayes’s formula

$P (B_{j} | A) = \frac{P (A | B_{j}) P (B_{j})}{P (A)}$

law of total probability $P (A)$

$P (A) = P (A | B_{1}) P (B_{1}) + \dots + P (A | B_{n}) P (B_{n}) .$

7.1.5 Random variables and distribution functions

Random variable takes on different values determined by chance. we can use random variables’ mathematical (distribution) function to find their probability.

probability mass function (PMF, discrete), e.g. Binomial Distribution. upon some conditions are satisfied, the sampling distribution of the sample proportion is approximately normal.
Probability Density Function (PDF, continuous), e.g. normal distribution, t, chi-squre, f…
Cumulative Distribution Function (CDF).

7.1.6 Probability distribution

joint distribution, discrete variables $P (X = x_{i}, Y = y_{j}) = p_{i j}, i, j = 1, 2, \dots$ Marginal distribution, discrete variables $P (X = x_{i}) = \sum_{j = 1}^{\infty} p_{i j} = p_{i}, i = 1, 2, \dots$ conditional probability, discrete variables $P (Y = y_{j} ∣ X = x_{i}) = \frac{p_{i j}}{p_{i}}, j = 1, 2, \dots$

7.1.7 Conditional expectation

Conditional expectation is the mathematical expectation of a conditional distribution.

The discrete variable

$E (Y | X_{i}) = \sum_{i = 1}^{N} (Y_{i} | X_{i}) \cdot p (Y_{i} | X_{i})$

The continuous variable

$E (Y | X) = \int (Y | X) \cdot g (Y | X) d Y$

expectation formula, discrete variable $μ = E (X) = \sum x_{i} f (x_{i})$

7.1.8 Conditional variance

variance formula, discrete variable $σ^{2} = Var (X) = \sum (x_{i} - μ)^{2} f (x_{i})$

Conditional expectation and conditional variance exist and can be estimated by regression models.

7.1.9 Sampling

We make inferences about the population based on the sample (inference) after summarizing data (description).

The error is resulting from using a sample characteristic (statistic) to estimate a population characteristic (parameter).

Standard Error $S D (\bar{X}) = S E (\bar{X}) = \frac{σ}{\sqrt{n}}$

Central limit theorem and law of large numbers

For a large sample size, x mean is approximately normally distributed, regardless of the distribution of the population one samples from. so, the population parameter can be estimated using the sample.
With large samples, The mean of the sampling distribution is very close to the population mean.

7.1.10 Confidence interval

The higher the confidence level, the wider the width of the interval and thus the poorer the precision.

$point estimate \pm M \times \hat{S E} (estimate)$ the margin of error $E = z_{α / 2} \sqrt{\frac{\hat{p} (1 - \hat{p})}{n}}$

7.1.11 Introduction to Hypothesis Testing

-Set up the hypotheses and decide on the significance level.

-Construct and calculate the test statistic.

-Calculate probability value (p-value).

-Make a decision and state an overall conclusion.

7.2 Probability R practice

pros: don’t need complicated probability theory, easy (simulation)
cons: hard to get the exact solution

7.2.1 Integrate

integrate(function(x){x^2},0,2)$value

## [1] 2.666667

7.2.2 Derivation

fxy = expression(2*x^2+y+3*x*y^2)
dxy = deriv(fxy, c("x", "y"), func = TRUE)
dxy(1,2)

## [1] 16
## attr(,"gradient")
##       x  y
## [1,] 16 13

7.2.3 Create random variables with specific distributions

 dnorm(0)# density at a number

## [1] 0.3989423

 pnorm(1.28)# cumulative possibility

## [1] 0.8997274

 qnorm(0.95)#  quantile

## [1] 1.644854

 rnorm(10)# random numbers

##  [1] -0.3653699  1.1505794  0.3318688  0.3599051 -0.3353245 -0.1786117
##  [7] -1.3081370 -0.2332866 -0.4728839 -0.3887392

using covariance matrix to generate Gaussian multiple variables

 library(MASS)
 Sigma <- matrix(c(10,3,3,2),2,2)
 mvrnorm(n=20, rep(0, 2), Sigma)

1.4484169	1.9520869
-0.2309407	-0.4842930
-7.2353608	-0.6204178
4.4589251	1.8085832
-0.7333944	-1.1341429
-0.6655039	-0.9901418
1.0627694	-1.1316420
2.0981615	0.2361394
-6.0864836	-2.3473660
1.4420683	-1.1497685
-1.9555996	-0.4922280
0.5804978	1.5248606
-2.8239379	-1.1811420
4.1494135	1.4543936
-1.4067470	0.0285627
-0.5245873	-1.0248724
1.1966051	0.7503701
0.5866985	-1.2388653
-1.4909270	1.0553603
-1.5332388	-0.9982745

7.2.4 Prob function

pnorm(1.96,    0,1)

## [1] 0.9750021

qnorm(0.025,    0,1)

## [1] -1.959964

pchisq(3.84,1,lower.tail=F)

## [1] 0.05004352

mean(rchisq(10000,1)>3.84) #simulation

## [1] 0.0509

7.2.5 Vector and operations

seq(1,10,  2)

## [1] 1 3 5 7 9

x=rep(1:3,6)
x

##  [1] 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3

y=rep(1:3, each = 6)
y

##  [1] 1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3

x+y

##  [1] 2 3 4 2 3 4 3 4 5 3 4 5 4 5 6 4 5 6

x-y

##  [1]  0  1  2  0  1  2 -1  0  1 -1  0  1 -2 -1  0 -2 -1  0

x*y

##  [1] 1 2 3 1 2 3 2 4 6 2 4 6 3 6 9 3 6 9

x/y

##  [1] 1.0000000 2.0000000 3.0000000 1.0000000 2.0000000 3.0000000 0.5000000
##  [8] 1.0000000 1.5000000 0.5000000 1.0000000 1.5000000 0.3333333 0.6666667
## [15] 1.0000000 0.3333333 0.6666667 1.0000000

x%*%y

7.2.6 Select and substitute elements of vector

x[c(2,3)]

## [1] 2 3

x[-1]

##  [1] 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3

x[x>2]

## [1] 3 3 3 3 3 3

x[x==2]

## [1] 2 2 2 2 2 2

# substitute 
x[x == 2] <- 0.5
x

##  [1] 1.0 0.5 3.0 1.0 0.5 3.0 1.0 0.5 3.0 1.0 0.5 3.0 1.0 0.5 3.0 1.0 0.5 3.0

7.2.7 Matrix and operations

matrix(1:10,2,5)

1	3	5	7	9
2	4	6	8	10

matrix(1:10,5,2)

1	6
2	7
3	8
4	9
5	10

a <- matrix(12:20,3,3)
a[2,]

## [1] 13 16 19

a[,2]

## [1] 15 16 17

a[-2,]

12	15	18
14	17	20

a[,-2]

12	18
13	19
14	20

a[2,1]=21
a

12	15	18
21	16	19
14	17	20

7.2.8 Compute inverse, determinant and eigen values of matrix

a<-matrix(c(11,21,31,21,32,43,12,32,54),3,3)
solve(a)

-1.9775281	3.471910	-1.6179775
0.7977528	-1.247191	0.5617978
0.5000000	-1.000000	0.5000000

det(a)

## [1] -178

solve(a)*det(a)

352	-618	288
-142	222	-100
-89	178	-89

t(a)

11	21	31
21	32	43
12	32	54

eigen(a)

## eigen() decomposition
## $values
## [1] 91.6892193  5.6541299 -0.3433491
## 
## $vectors
##            [,1]       [,2]       [,3]
## [1,] -0.2573423 -0.7530908 -0.9049786
## [2,] -0.5253459 -0.1712782  0.3538153
## [3,] -0.8110405  0.6352306  0.2362806

7.2.9 Dataframe

name<-c('A','B','C')
chinese<-c(92,96,95)
math<-c(86, 85, 92)
score<-data.frame(name, chinese, math)
score

name	chinese	math
A	92	86
B	96	85
C	95	92

score[2]

chinese
92
96
95

score$math

## [1] 86 85 92

7.2.10 Solve problems using simulation

for loop

sim<-10000
p<-numeric(sim)
# numeric=NULL
for (i in 1:sim){
  p[i]<-  abs(mean(rnorm(10,20,sqrt(3)))-mean(rnorm(15,20,sqrt(3))))<0.1
}

mean(p)

## [1] 0.115

using replicate

mean(replicate(10000,abs(mean(rnorm(10,20,sqrt(3)))-mean(rnorm(15,20,sqrt(3))))<0.1))

## [1] 0.107

using apply function

A<-matrix(rnorm(250000,  20,sqrt(3)),10000,25)
head(A)

19.11360	18.99439	20.54412	20.26354	19.34949	22.84288	23.22408	19.08958	21.36533	16.99797	21.07603	17.90465	17.81727	21.05390	22.45935	17.25351	21.64149	24.64879	21.36324	22.67676	22.58186	19.95328	17.95461	18.67138	22.23283
21.50961	19.31161	18.32036	18.46718	21.48844	17.24305	21.24674	23.85790	18.82467	22.02443	19.79884	21.64527	19.01461	20.35104	19.20876	19.58578	19.66980	22.70219	21.19677	18.13026	18.93463	19.30829	18.91371	18.38888	21.97849
18.69794	20.80376	24.43204	19.16716	22.83998	19.55858	19.76341	18.29125	17.73783	20.24857	19.64368	20.84156	18.11681	18.38696	21.80904	18.04138	19.79941	19.41351	23.71580	15.86155	18.15329	18.68470	23.16201	20.39224	19.73438
18.12514	20.01039	20.65357	17.95539	20.94095	21.32920	18.43275	19.36403	20.40667	22.44249	20.62391	21.00531	20.72527	19.32363	21.83892	18.74153	18.25122	20.79259	21.83469	19.16572	18.88338	18.85391	18.57082	20.26071	22.59657
18.34587	20.09544	20.29301	18.90707	23.30686	18.02567	19.96716	18.88519	23.80685	21.16138	18.78506	16.14750	24.74161	19.72238	17.32301	21.29658	20.40909	21.22702	23.87678	19.59053	19.86434	19.36097	19.61389	21.79788	20.07856
19.67138	18.17042	18.06493	22.68991	21.33451	18.99442	19.96875	21.50483	22.22520	22.84398	19.96615	23.50315	18.44274	19.28381	22.26025	19.53599	19.83414	19.74906	20.09022	18.37966	19.40200	20.11609	16.40877	19.09474	20.22407

f<-function(x)   {abs(mean(x[1:10])-mean(x[11:25]))}
# solve the mean by apply

mean(apply(A,1,f)>0.1)

## [1] 0.8898

using probability method

 pnorm(0.1,0,sqrt(0.5))-pnorm(-0.1,0,sqrt(0.5))

## [1] 0.1124629

7.2.11 Permutations and combinations

choose(10,2)

## [1] 45

# combn(10,2)
factorial(10)

## [1] 3628800

prod(1:10)

## [1] 3628800

7.2.12 Search value position in vector

a<-c(1,2,3,5,0,9)
which(a==min(a))

## [1] 5

sum(a)

## [1] 20

unique(a)

## [1] 1 2 3 5 0 9

length(a)

## [1] 6

min(a)

## [1] 0

max(a)

## [1] 9

all(c(3,4) %in% a)

## [1] FALSE

7.2.13 Solve directly and optimize

plot and find the range of solve

f<-function(x){x^2-exp(x)} 
uniroot(f,c(-0.8,-0.6))  $root

## [1] -0.7034781

f2<-function(x){abs(x^2-exp(x))} 
optimize   (f2,lower=-0.8,upper=-0.6)$minimum

## [1] -0.703479

7.2.14 Calculate probability using simulation method

questions: randomly select 3 numbers out of 1:10, the sum is 9.

badge<-1:10 
sim<-10000 
p<-numeric(sim) 

for (i in 1:sim){ a<-sample(badge,3,replace=F) 
p[i]<-sum(a)==9 }

mean(p)

## [1] 0.0241

questions: eat three flavors tangyuan.

Tangyuan<-c(rep('A',8),rep('B',8),rep('C',8))
sim<-10000
p<-numeric(sim)
# how to do it according to the condition
for (i in 1:sim){
  a<-sample(Tangyuan,24,replace=F)
  p[i]<-(length(unique(a[1:6]))==3)&(length(unique(a[7:12]))==3)&(length(unique(a[13:18]))==3)&(length(unique(a[19:24]))==3)
}
mean(p)

## [1] 0.4838

question: select 2 balls when they are the same color.

box1<-c(rep('white',5), rep("black",11), rep('red',8))
box2<-c(rep('white',10), rep("black",8), rep('red',6))
sim<-10000
p<-numeric(sim)

for (i in 1:sim){
  a<-sample(box1, 1)
  b<-sample(box2, 1)
  p[i]<- a==b
}
mean(p)

## [1] 0.3274

select after putting them back

box<-c(rep("white",4),rep("red",2))
sim<-10000
t<-numeric(sim)

for (i in 1:sim){
  a<-sample(box, 2 ,replace=T)
  #  there are two white balls
  t[i]<-length(a[a=="white"])==2
}
mean(t)

## [1] 0.4447

question: two students have the same birthday out of 30 students

n<-30
sim<-10000
t<-numeric(sim)

for (i in 1:sim){
  a<-sample(1:365, n, replace=T)
  t[i]<-n-length(unique(a))
}
1-mean(t==0)

## [1] 0.7015

#  probability
1-prod(365:(365-30+1))/365^30

## [1] 0.7063162

An event is a set of outcomes. You can describe certain events using random variables (x, distribution). the distribution of random variable function.

7.2.15 Discrete random variable

question: choose correct one out of four answers

x<-0:5
y<-dbinom(x,5,1/4)
plot(x,y,col=2,type='h')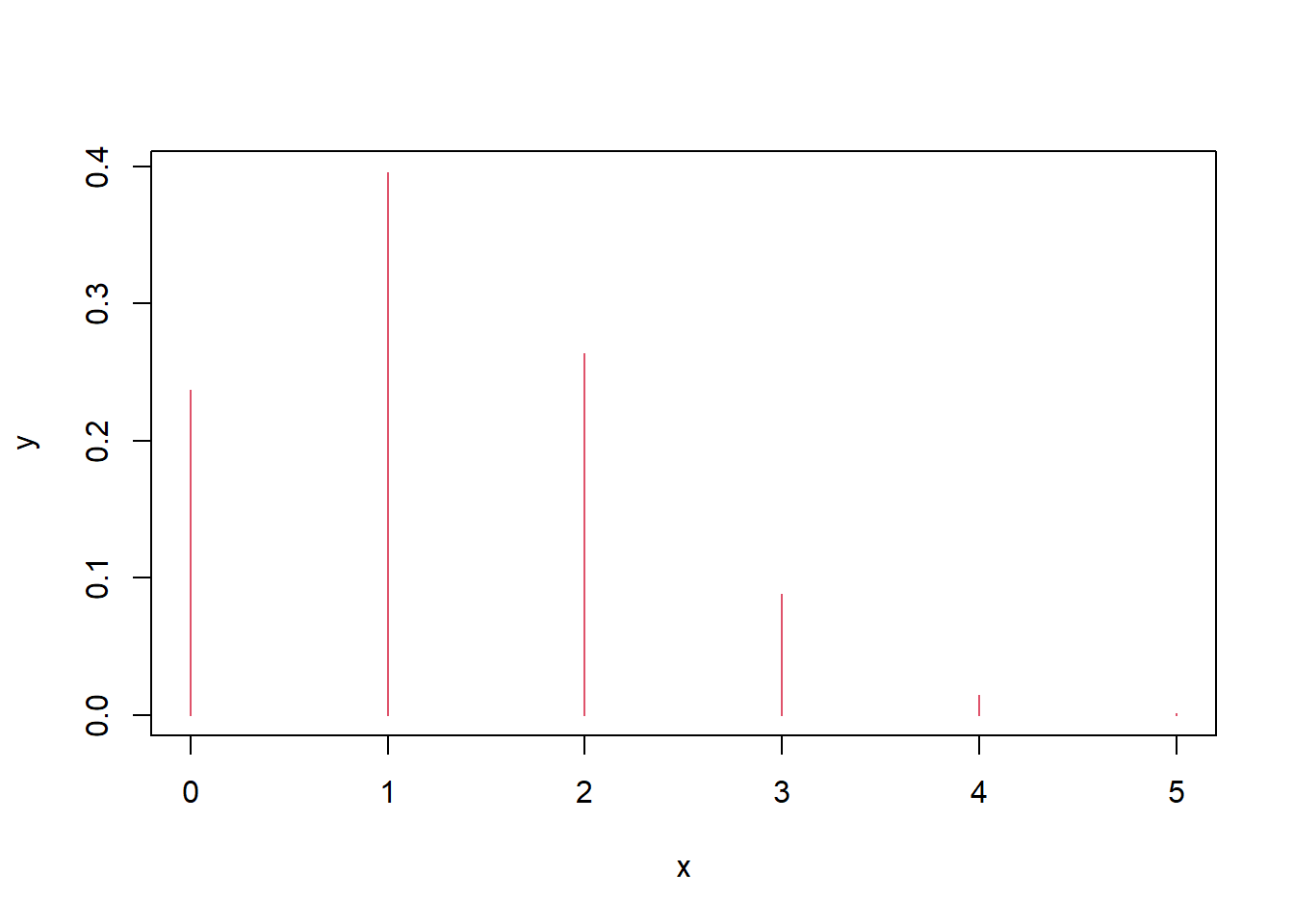

using plot the probability of shooting is 0.02, what is the most likelihood of hit with 400 shootings

k<-0:400
p<-dbinom(k,400,0.02)
plot(k,p,type='h',col=2)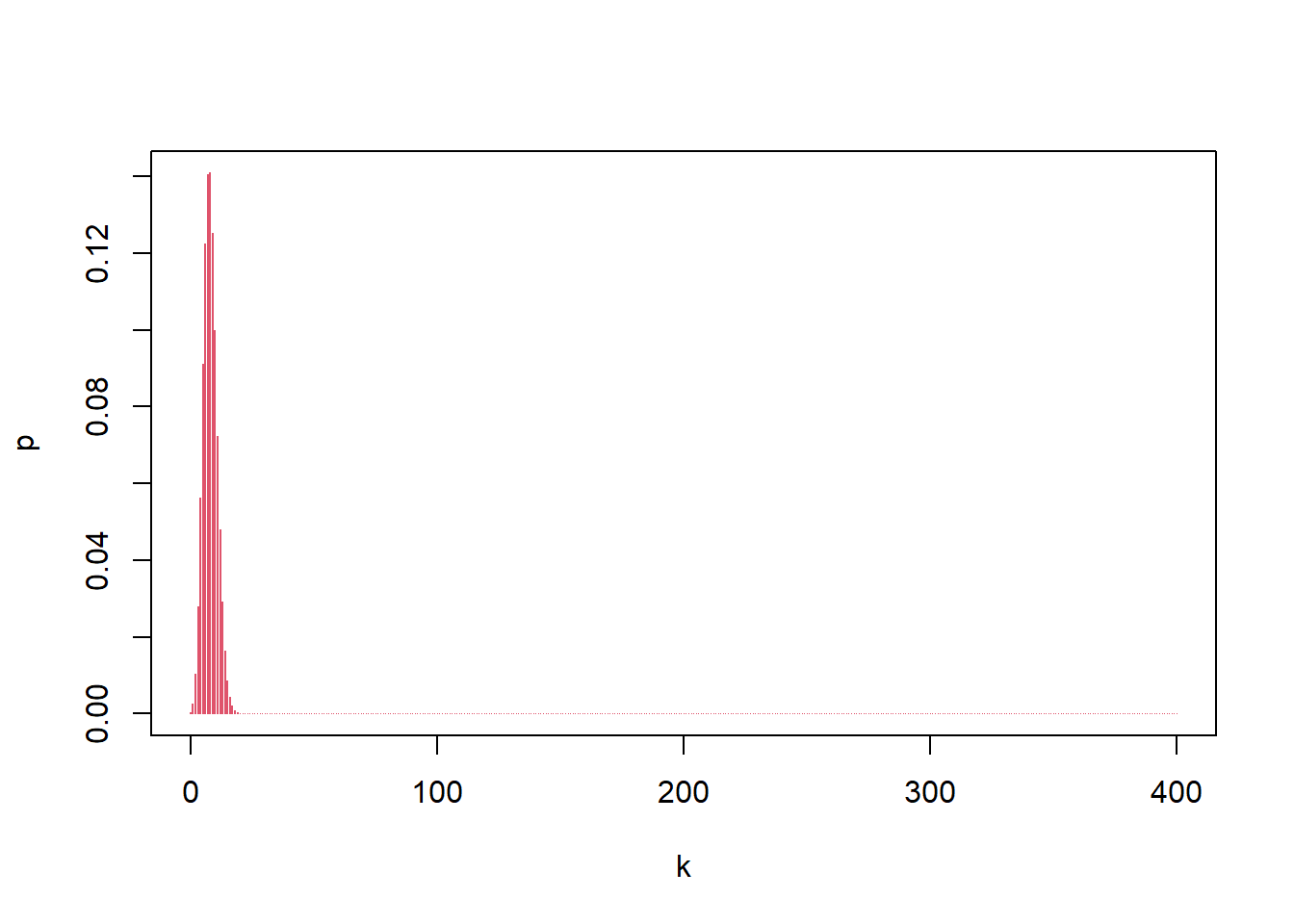

plot(k,p,type='h',col=2,xlim=c(0,20))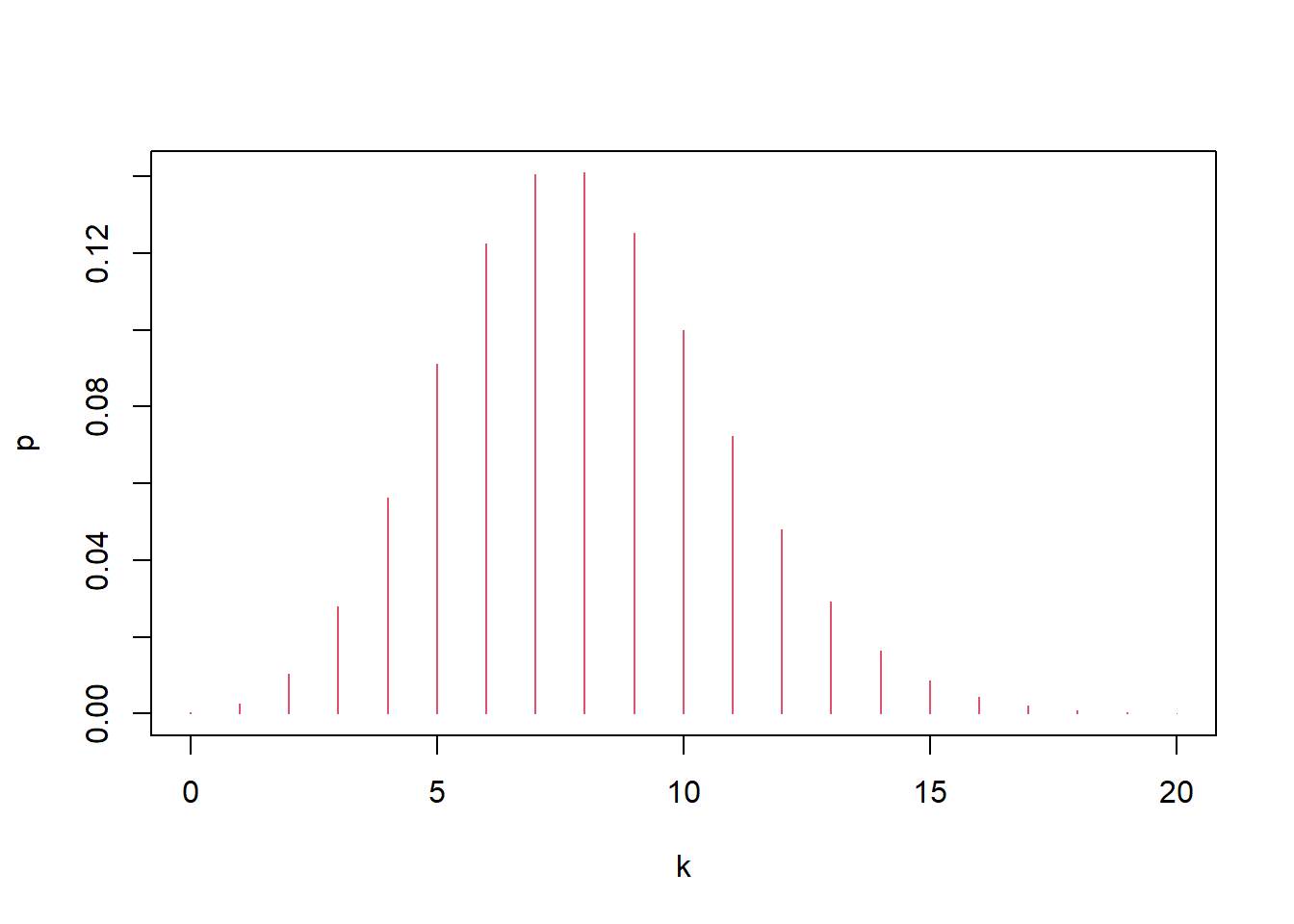

dbinom(7,400,0.02)

## [1] 0.1406443

dbinom(8,400,0.02)

## [1] 0.1410031

7.2.16 Exponent distribution

question: lifetime of a light (lamda=1/2000)

integrate(dexp,rate=1/2000,1000,Inf)$value

## [1] 0.6065307

f<-function(x){dexp(x,rate=1/2000)}
integrate(f,1000,Inf) $value

## [1] 0.6065307

1-pexp(1000,rate=1/2000)

## [1] 0.6065307

mean(rexp(10000,rate=1/2000)>1000)

## [1] 0.6014

7.2.17 Normal distribution plot

continue variable

x<-seq(-3,3,0.01)
plot(x, dnorm(x,mean=0, sd=2),type="l",xlab="x",ylab = "f(x)", col=1,lwd=2,ylim=c(0,1))   #density function

lines(x, dnorm(x,mean=0, sd=1),lty=2, col=2,lwd=2)

lines(x, dnorm(x,mean=0, sd=0.5), lty=3,col=3,lwd=2)

exbeta<-c(expression(paste(mu,"=0,", sigma,"=2")), expression(paste(mu,"=0,",sigma,"=1")), expression(paste(mu,"=0,", sigma,"=0.5")))
legend("topright", exbeta, lty = c(1, 2,3),col=c(1,2,3),lwd=2)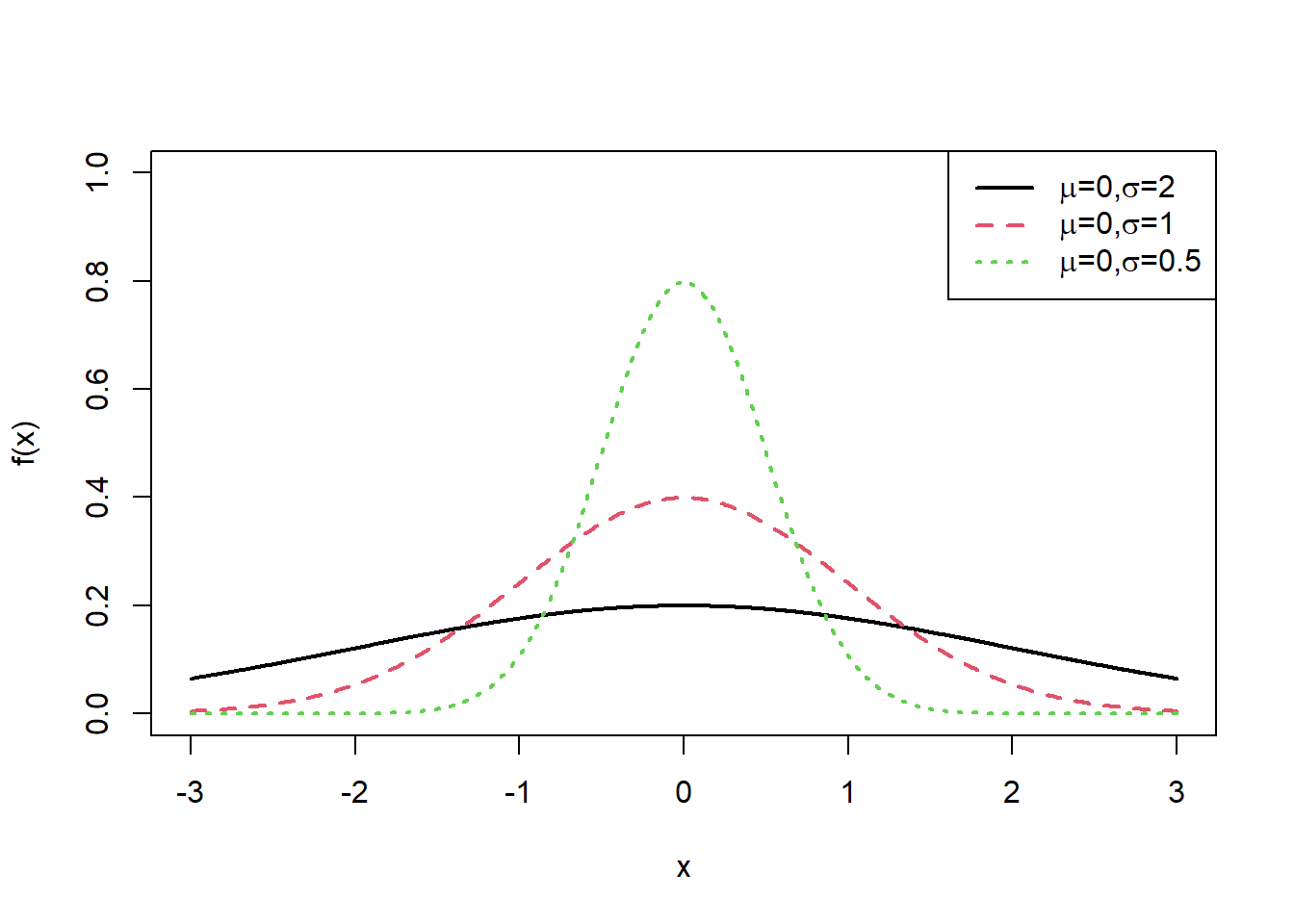

x<-seq(-3,3,0.01)
plot(x, dnorm(x,mean=-1, sd=1),type="l",xlab="x",ylab = "f(x)", col=1,lwd=2,ylim=c(0,0.6))
lines(x, dnorm(x,mean=0, sd=1),lty=2, col=2,lwd=2)
lines(x, dnorm(x,mean=1, sd=1), lty=3,col=3,lwd=2)
exbeta<-c(expression(paste(mu,"=-1,", sigma,"=1")), expression(paste(mu,"=0,",sigma,"=1")), expression(paste(mu,"=1,", sigma,"=1")))
legend("topright", exbeta, lty = c(1, 2,3),col=c(1,2,3),lwd=2)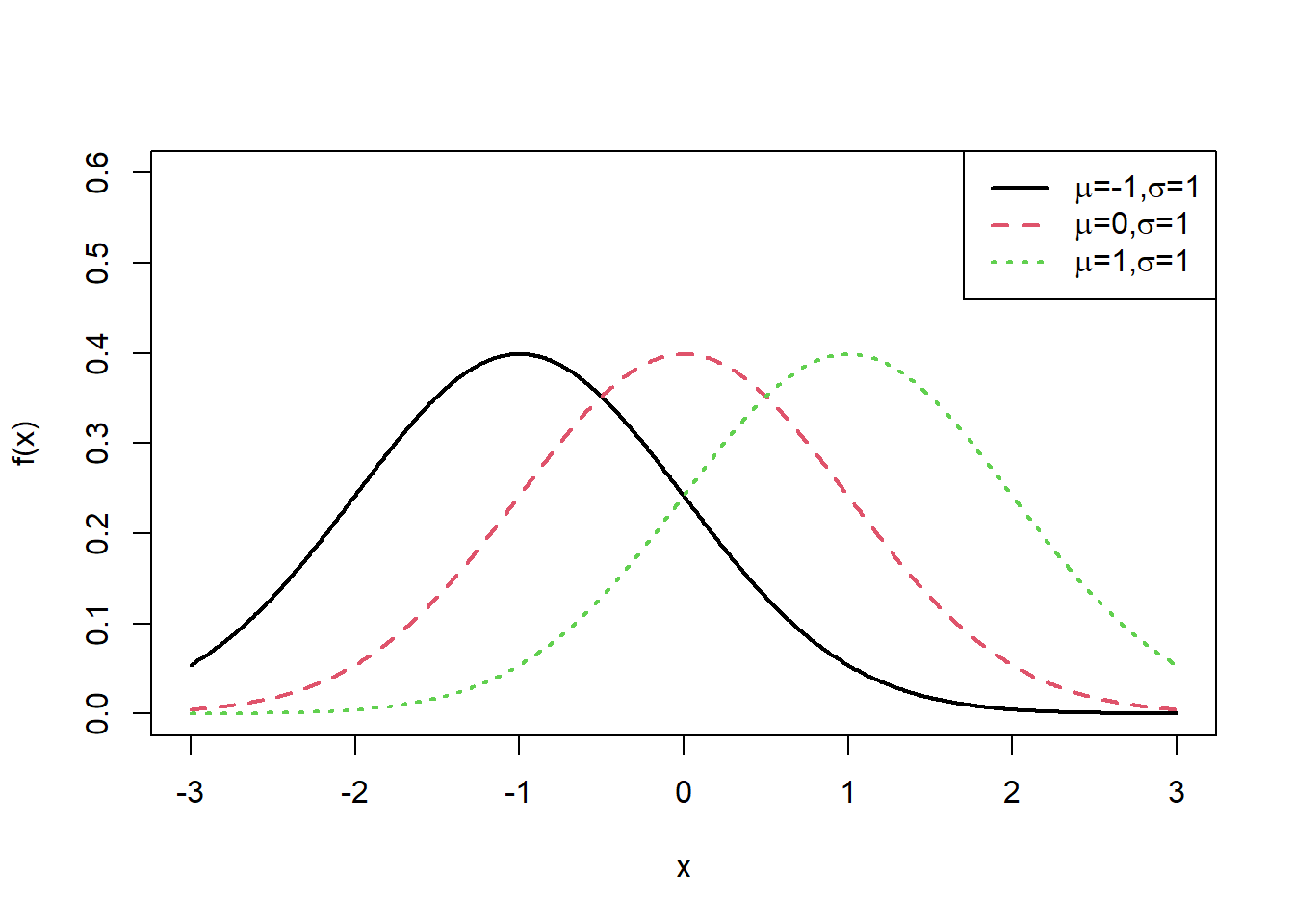

question: solve sigma using nomoral distribution

sigma<-1
repeat{
sigma<-sigma+0.01
if (pnorm(200,160,sigma)-pnorm(120,160,sigma)<0.80) break
}
sigma

## [1] 31.22

# alternative 
sigma<-1
while( pnorm(200,160,sigma)-pnorm(120,160,sigma)>=0.80){sigma<-sigma+0.01}
sigma

## [1] 31.22

7.2.18 Distribution of random variable function

qestion: x^2 and 2x distributions

x<-c(-1,0,1,2,2.5)
weight<-c(0.2,0.1,0.1,0.3,0.3)
toss<-sample(x,10000,replace=T,weight)
table(toss^2)/length(toss^2)

0	1	4	6.25
0.1026	0.2963	0.2998	0.3013

table(2*toss)/length(2*toss)

-2	0	2	4	5
0.201	0.1026	0.0953	0.2998	0.3013

quetsion: continous vairable density

x <- seq(0,5,0.01)
truth<-rep(0,length(x))
truth[0<=x&x<1]<-2/3
truth[1<=x&x<2]<-1/3

plot(density(abs(runif(1000000,-1,2))),main=NA, ylim=c(0,1),lwd=3,lty=3)

lines(x,truth,col="red",lwd=2)
legend("topright",c("True Density","Estimated Density"), col=c("red","black"),lwd=3,lty=c(1,3))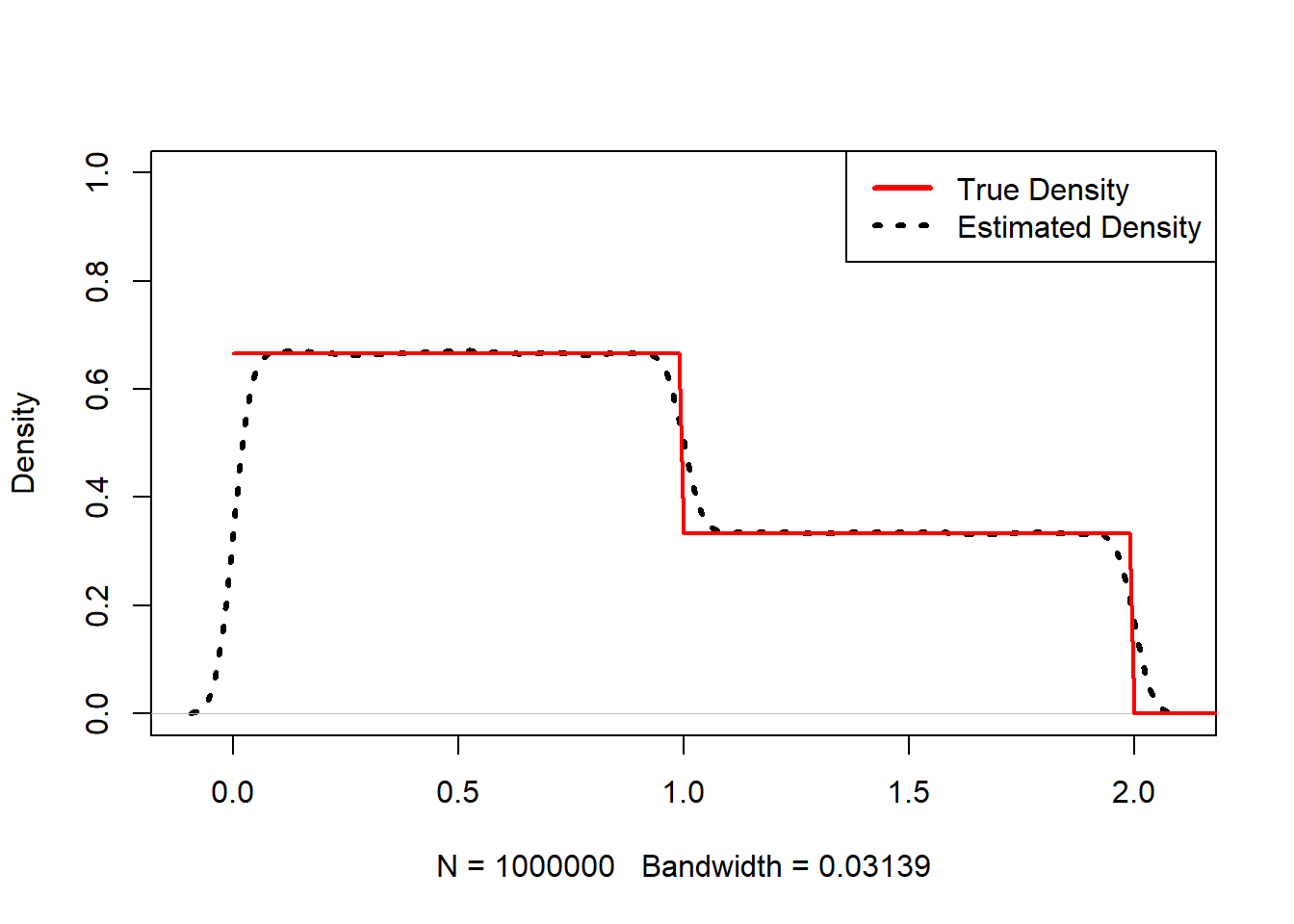

7.2.19 Join and margin probability

question: x is randomly selected from 1:4, y randomly select from x

p<-function(x,y) {
sim<-10000
t<-numeric(sim)
for (i in 1:sim) {
a<-sample(1:4,1)
b<-sample(1:a,1)
t[i]<-(a==x)&(b==y) }
mean(t)
}
PF<-matrix(0,4,4)
for (i in 1:4) {
for (j in 1:4) {
PF[i,j]<-p(i, j) } }
PF

0.2438	0.0000	0.0000	0.0000
0.1216	0.1226	0.0000	0.0000
0.0838	0.0831	0.0855	0.0000
0.0637	0.0645	0.0634	0.0626

apply(PF,1,sum)

## [1] 0.2438 0.2442 0.2524 0.2542

apply(PF,2,sum)

## [1] 0.5129 0.2702 0.1489 0.0626

7.2.20 Multiple random variables plots

2 discrete variables distribution

x<-sample(1:4, 10000, replace=T, prob=c(1/4, 1/4, 1/4, 1/4))
y<-numeric(10000)
for(i in 1:10000) {
if(x[i]==1) {y[i]<-sample(1:4,1,replace=T, prob=c(1,0,0,0))}
if(x[i]==2) {y[i]<-sample(1:4,1,replace=T, prob=c(1/2,1/2,0,0))}
if(x[i]==3) {y[i]<-sample(1:4,1,replace=T, prob=c(1/3,1/3,1/3,0))}
if(x[i]==4) {y[i]<-sample(1:4,1,replace=T, prob=c(1/4,1/4,1/4,1/4))}
}
z1<-x+y
table(z1)/length(z1)

2	3	4	5	6	7	8
0.2496	0.1222	0.2143	0.1421	0.1473	0.0642	0.0603

z2<-x*y
table(z2)/length(z2)

1	2	3	4	6	8	9	12	16
0.2496	0.1222	0.0869	0.1897	0.0798	0.066	0.0813	0.0642	0.0603

z3<-pmax(x,y)
table(z3)/length(z3)

1	2	3	4
0.2496	0.2496	0.248	0.2528

z4<-x/y
table(z4)/length(z4)

1	1.33333333333333	1.5	2	3	4
0.5186	0.0642	0.0798	0.1882	0.0869	0.0623

two normal distributions X～N(0,1),Y～N(0,1), Z=X+Y, therefre Z~N(0,2)

Z<-function(n){
x<-seq(-4,4,0.01)
truth<-dnorm(x,0,sqrt(2))

plot(density(rnorm(n)+rnorm(n)),main="Density Estimate of the Normal Addition Model",ylim=c(0,0.4),lwd=2,lty=2)

lines(x,truth,col="red",lwd=2)
legend("topright",c("True","Estimated"),col=c("red","black"),lwd=2,lty=c(1,2))
}

Z(10000)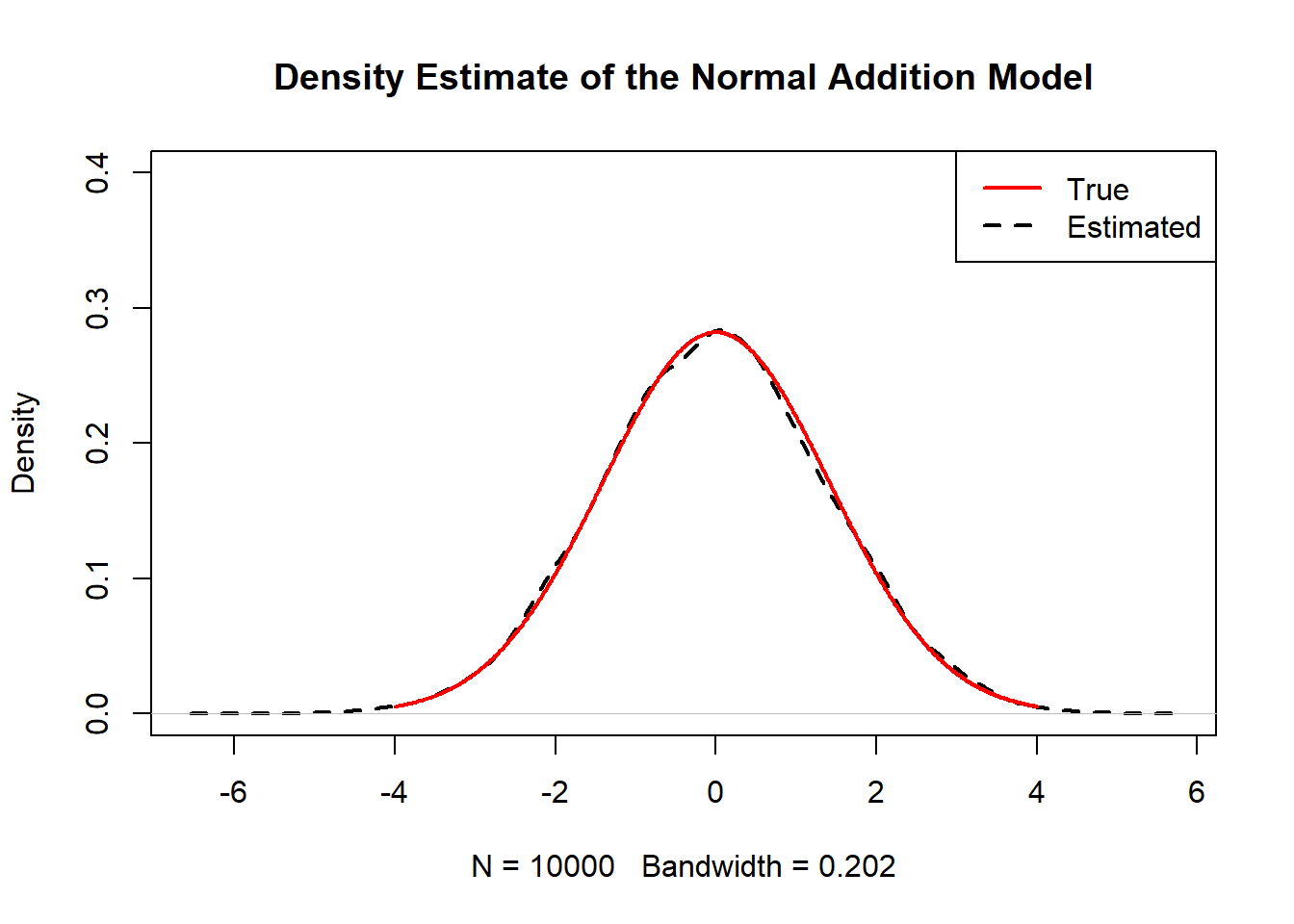

7.2.21 Generate a circle using simulated random dots

D={(x,y)|x^2 + y^2 <= 1}

x<-runif(10000,-1,1)
y<-runif(10000,-1,1)

a<-x[x^2+y^2<=1]
b<-y[x^2+y^2<=1]
plot(a,b,col=4)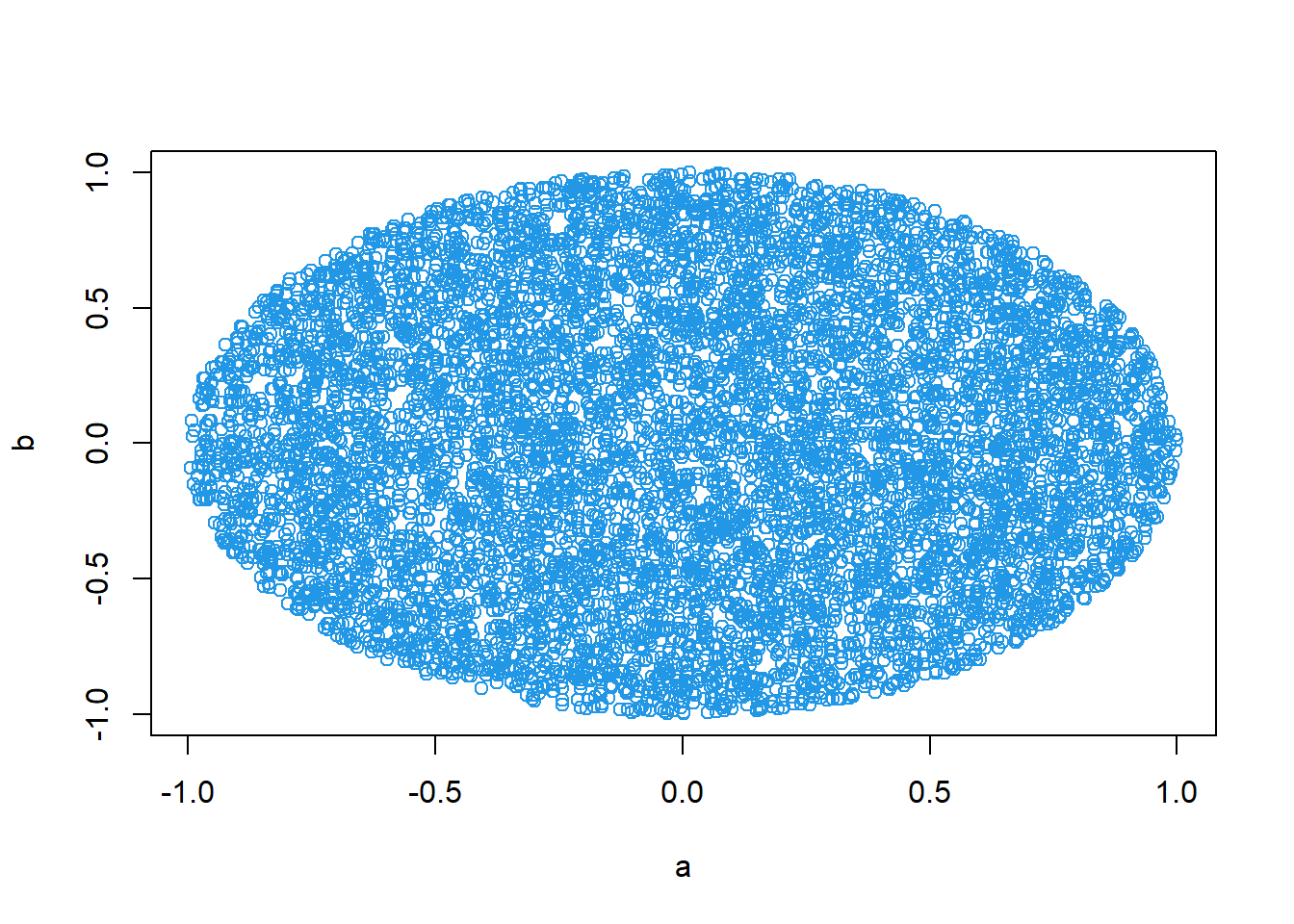

oval

a<-3
b<-1
x<-runif(10000,-a,a)
y<-runif(10000,-b,b)
x1<-x[x^2/a^2+y^2/b^2<=1]
y1<-y[x^2/a^2+y^2/b^2<=1]
plot(x1,y1,col=3)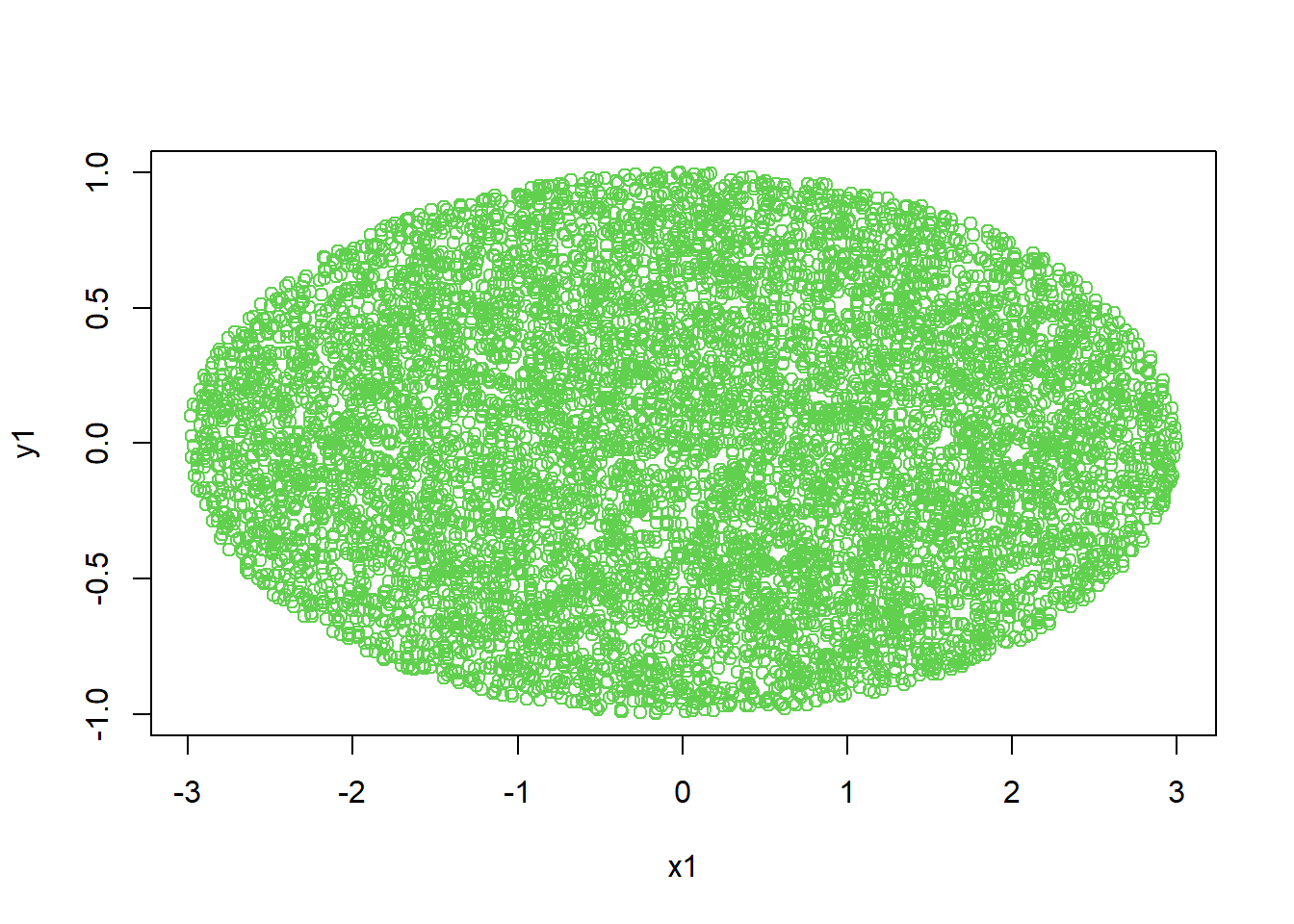

7.2.22 Expectation

discrete variable question: the benefit of products is different.

sim<-10000
t<-numeric(sim)

for (i in 1:sim) {
Y<-1500
X<-rexp(1,rate=1/10)

Y[1<X&X<=2]<-2000
Y[2<X&X<=3]<-2500
Y[3<X]<-3000
t[i]<-Y
}

mean(t)

## [1] 2734.6

continue variable

7.2.23 Central Limit Theorem

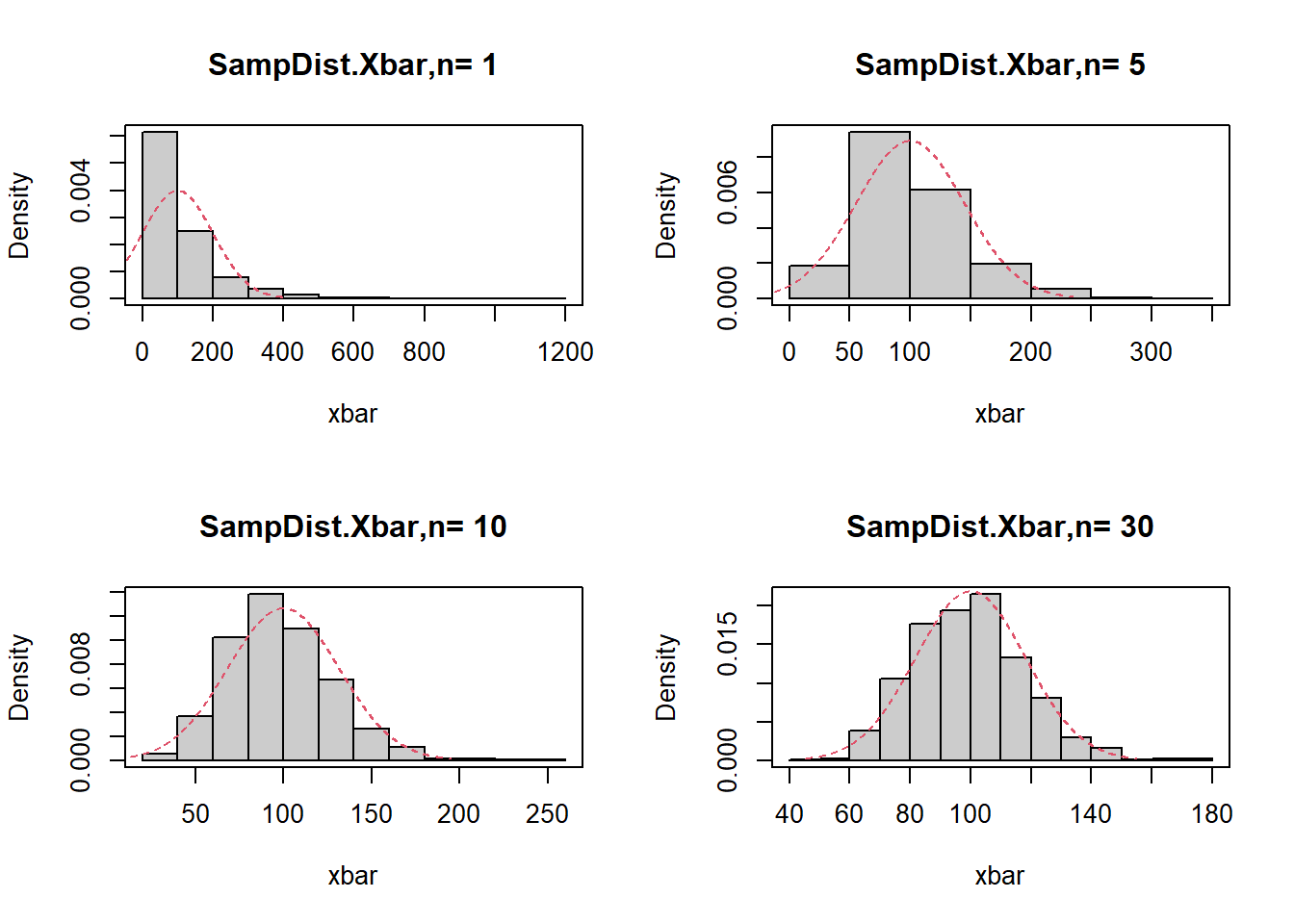
###Central Limit Theorem for Expotential distribution
layout(matrix(c(1,3,2,4 ),ncol=2))
r<-1000
lambda<-1/100

for (n in c(1,5,10,30)){
mu<-1/lambda
xbar<-numeric(r)
sxbar<-1/(sqrt(n)*lambda)

for(i in 1:r){
xbar[i]<-mean(rexp(n,rate=lambda))
}

hist(xbar,prob=T,main=paste('SampDist.Xbar,n=',n),col=gray(.8))
Npdf<-dnorm(seq(mu-3*sxbar,mu+3*sxbar,0.01),mu,sxbar)
lines(seq(mu-3*sxbar,mu+3*sxbar,0.01),Npdf,lty=2,col=2)
box()
}

#####The central limit theorem for uniform distribution
layout(matrix(c(1,3,2,4),ncol=2))
r<-10000
mu<-5
sigma<-10/sqrt(12)
for (n in c(1,5,10,30)){
xbar<-numeric(r)
sxbar<-sigma/sqrt(n)
for (i in 1:r){
xbar[i]<-mean(runif(n,0,10))}
hist(xbar,prob=T,main=paste('SampDist.Xbar,n=',n),col=gray(0.8),ylim=c(0,1/(sqrt(1*pi)*sxbar)))
XX<-seq(mu-3*sxbar,mu+3*sxbar,0.01)
Npdf<-dnorm(XX,mu,sxbar)
lines(XX,Npdf,lty=2,col=2)
box()}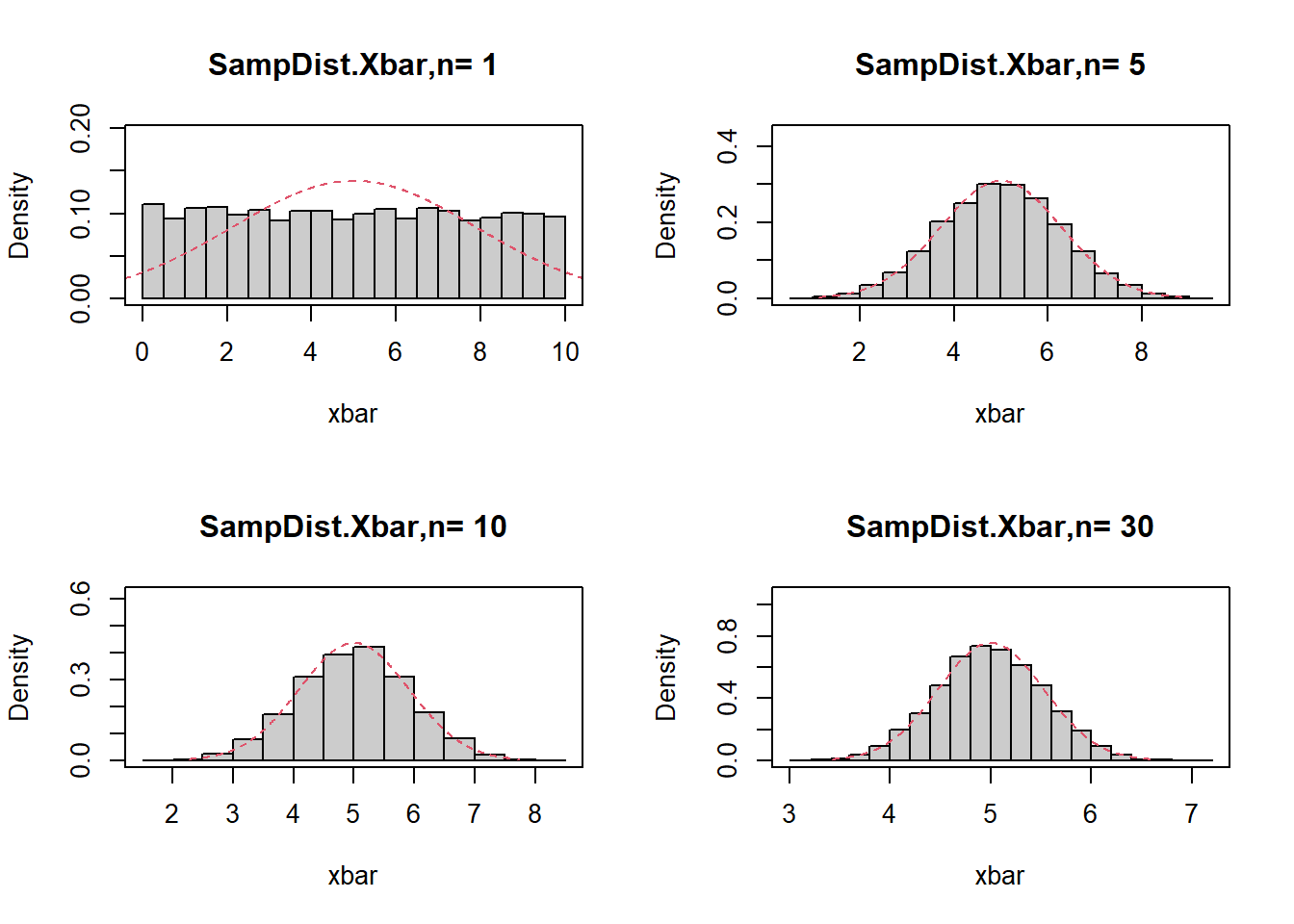

7.2.24 Law of large numbers

N <- 5000
set.seed(123) 

x <- sample(1:10, N,    replace = T)
s <- cumsum(x)    
r.avg <- s/(1:N)

options(scipen = 10)  

plot(r.avg, ylim=c(1, 10), type = "l", xlab = "Observations"
     ,ylab = "Probability", lwd = 2)
lines(c(0,N), c(5.5,5.5),col="red", lwd = 2)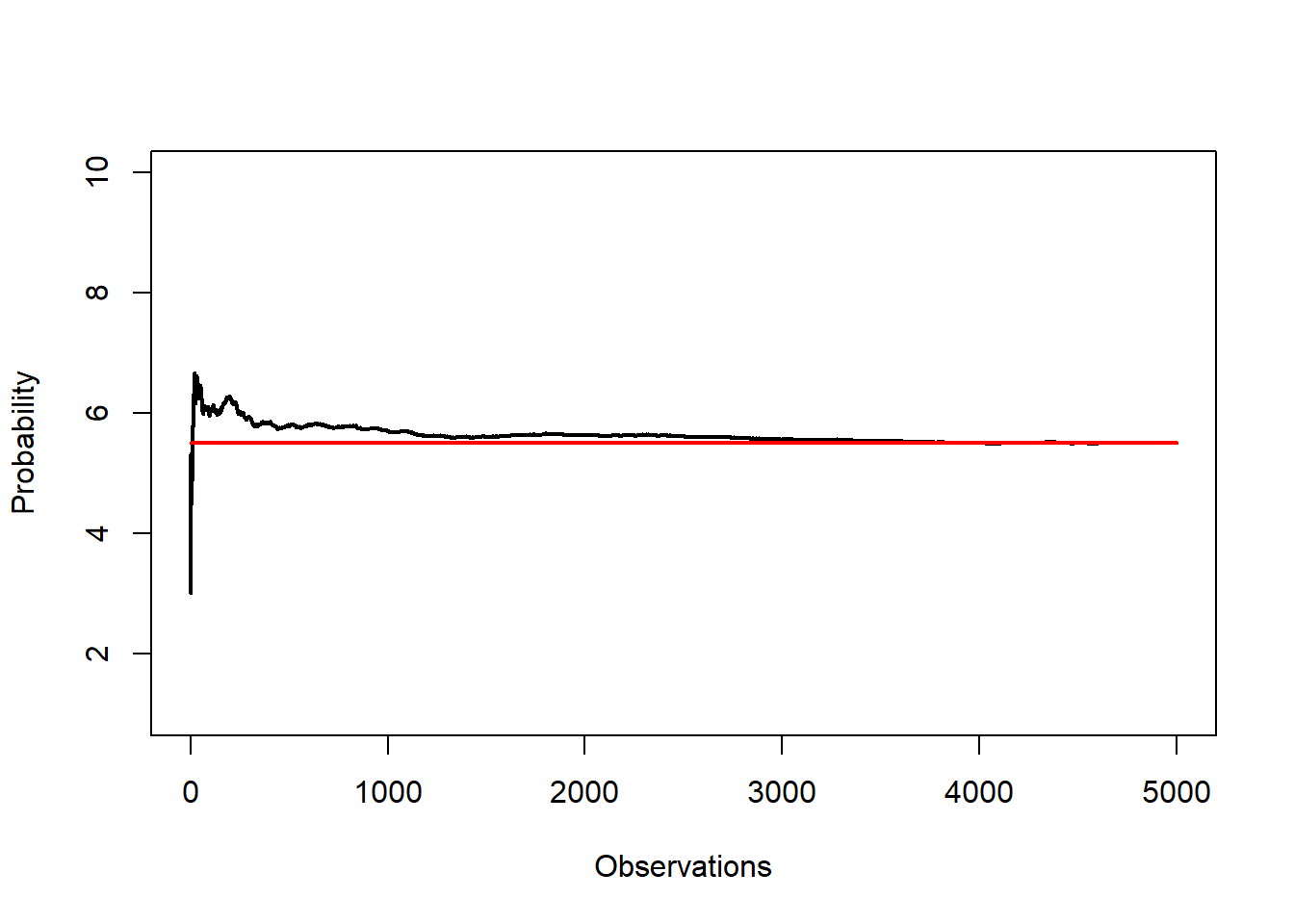

7.2.25 Empirical distribution

x<-c(-2,-1.2,1.5,2.3,3.5)
plot(ecdf(x),col=2)
abline(v=0,col=3)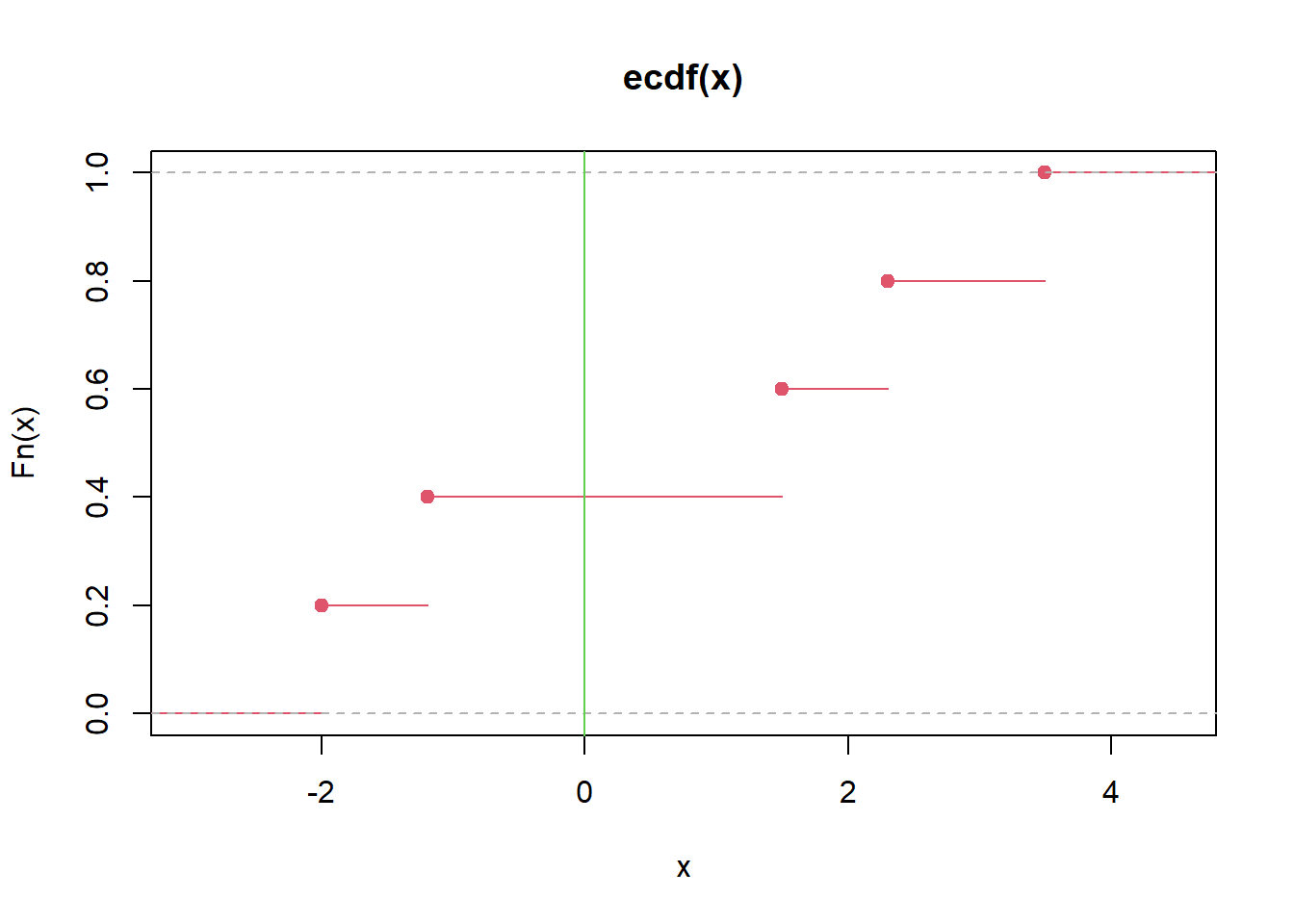

question: three numbers are from N(2,9), and what is the prob of their mean >3?

A<-matrix(rnorm(30000,2,3),10000,3)
mean(apply(A,1,mean)>3)

## [1] 0.2789

7.2.26 Maximum likelihood estimate

question: eatimate mean and variance

sample<-c(1.38, 3.96, -0.16, 8.12, 6.30, 2.61, -1.35, 0.03, 3.94, 1.11)
n<-length(sample)
muhat<-mean(sample)
sigsqhat<-sum((sample-muhat)^2)/n
muhat

## [1] 2.594

sigsqhat

## [1] 8.133884

loglike<-function(theta){
a<--n/2*log(2*pi)-n/2*log(theta[2])-sum((sample-theta[1])^2)/(2*theta[2])
return(-a)
}
optim(c(2,2),loglike,method="BFGS")$par

## [1] 2.593942 8.130340

7.2.27 t distribution, F distribution plots, and common distributions

n<-30
x<-seq(-6,6,0.01)
y<-seq(-6,6,1)

Truth<-df(x,1,n)

plot(density(rt(10000,n)^2),main="PDF",ylim=c(0,1),lty=2,xlim=c(-6,6)) #simulation 

lines(x, dt(x,n), col=3) #t dist
 
lines(x, dchisq(x,2), col=4) #chisq dist
 
lines(x,Truth,col=2) #f dist
abline (v=0 ,col=7)  

 
points(y,dbinom(y, size=12, prob=0.2),col=1) #binomial dist
points(y,dpois(y, 6),col=2) #poisson dist

lines(y,dunif(-6:6,min=-6,max=6 ),col=5) #uniform